In the first part of my blog post series about building a small clone of the classic arcade game Asteroids on top of Compose for Desktop, we saw how to implement the main game loop, as well as manage state and draw basic shapes. In this post, we will explore some more details of the game implementation. This includes:

  • Rendering details – making sure game objects don’t escape our play area, and using a device-independent coordinate system for rendering
  • Geometry and linear algebra – the secret sauce that makes the space ships fly
  • Frame-independent movement – so that our game works consistently.

Let’s learn about these topics!

Rendering: Clipping and Coordinate Systems

In the context of rendering, there are two areas that still need our attention – we need to make sure that our game objects are constrained to the game surface, and we need to make a conscious decision about the units of the coordinates we use to describe the position of a game object. We’ll discuss both in this section.

Clipping

By default, Compose naively draws your objects without any clipping. This means game objects can poke outside the “play surface”, which produces a weirdly fourth-wall-breaking effect:

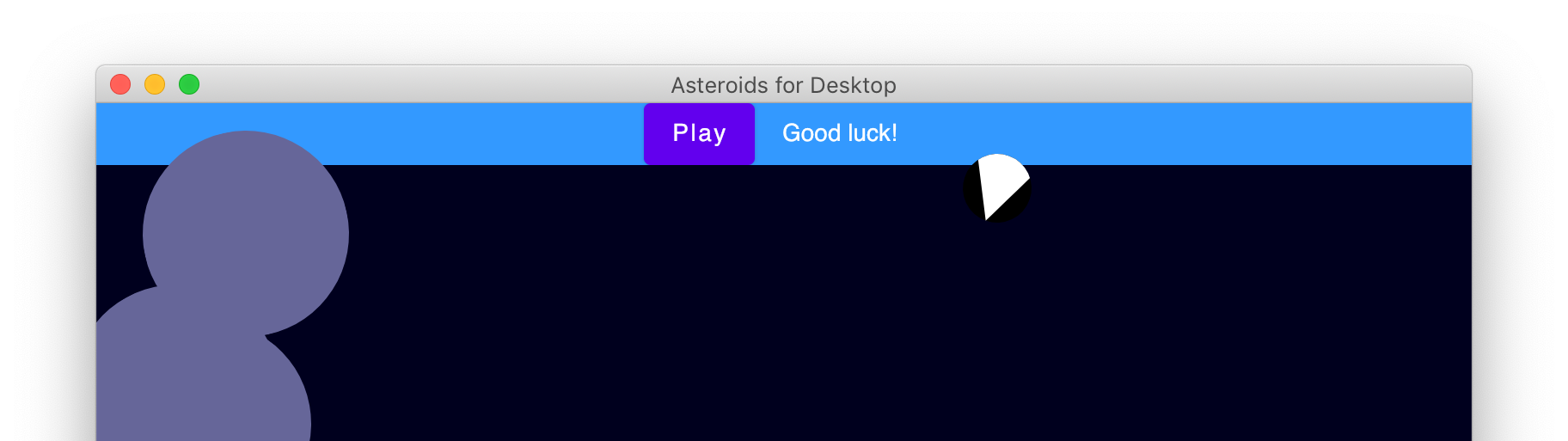
game objects escaping the bounds of reality

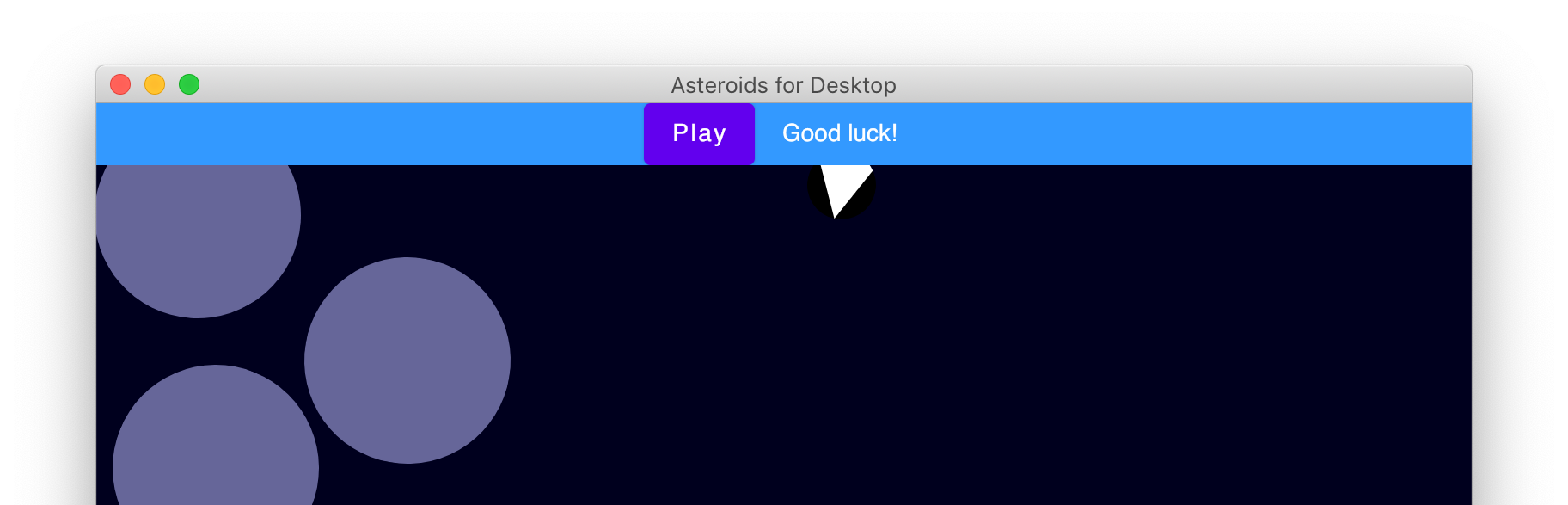
We constrain the game objects to the bounds of our play surface by applying Modifier.clipToBounds() to the Box which defines our play surface:

Box(modifier = Modifier
                .fillMaxWidth()
                .fillMaxHeight()
                .clipToBounds()
                // . . .

Because all our game elements are drawn as children of this play area Box, using this modifier causes the rendered entities inside it to be cut off at the edges (instead of being drawn over the surrounding user interface):

game objects staying snugly inside the play area

Device-Independent Pixels and Density

Something else to be aware of when doing any kind of rendering tasks in Compose for Desktop is to keep the units of measurement in the back of your mind.

Wherever I worked with coordinates, I decided to work in device-independent pixels:

  • The mouse pointer position is stored as a DpOffset
  • Game width and height are stored as Dps
  • Game objects are placed on the play surface using their .dp coordinates.

This helps the game work consistently across high-density displays and low-density displays alike. However, it also requires some operations to be performed in the context of Density.

For example, the pointerMoveFilter returns an Offset in pixels – and they are not device-independent!. To work around this, we obtain the local screen density in our composition:

val density = LocalDensity.current

We then use with(density) to access the toDp() extension functions to the Offset into a DpOffset, allowing us to store our targetLocation in this device-independent pixel format:

.pointerMoveFilter(onMove = {
    with(density) {
        game.targetLocation  = DpOffset(it.x.toDp(), it.y.toDp())
    }
    false
})

For storing the play area’s width and height, we do a very similar thing, just without wrapping it in a DpOffset:

.onSizeChanged {
    with(density) {
        game.width = it.width.toDp()
        game.height = it.height.toDp()
    }
}

A Game of Geometry and Linear Algebra

Underneath the visualization, the “Asteroids” game builds on just a few basic blocks to implement its mechanics – it is really a game of vectors and linear algebra:

  • The position, movement, and acceleration of the ship can be described by position, movement, and acceleration vectors.
  • The orientation of the ship is the angle of the vector between the ship and the cursor.
  • Circle-circle collisions can be tested based on distance vectors.

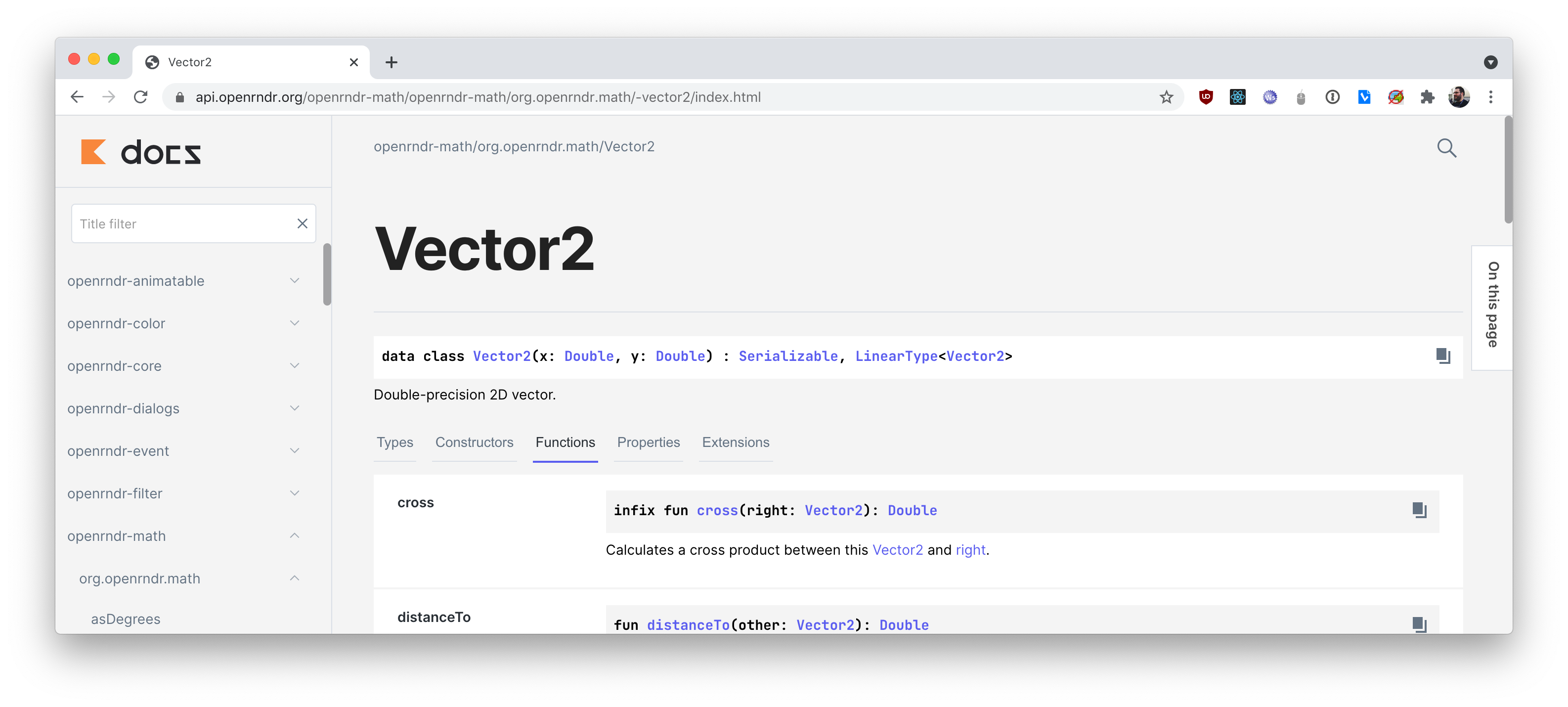
Instead of reinventing the wheel vector, I decided to use openrndr-math, which includes an implementation of the Vector2 class including all common operations, like scalar multiplication, addition, subtraction, the dot product, and more. (Ever since listening to the Talking Kotlin episode, I’ve been meaning to explore OPENRNDR in detail, but that will have to happen in a separate project.)

OPENRNDR Vector2

As somebody who happens to be a bit rusty with their linear algebra skills, I extended the functionality of the class a bit. For example, I defined the following extension function to allow me to access the angle a Vector2 in degrees between 0-360:

fun Vector2.angle(): Double {
    val rawAngle = atan2(y = this.y, x = this.x)
    return (rawAngle / Math.PI) * 180
}

Thankfully, I did not have to spend too much time on figuring out the call to atan2, because I previously watched one of Leland Richardson’s live streams where he also uses this function to calculate some angles.

Extensions like this one help me express ideas in ways I understand them myself – and hopefully still will a few months down the road.

I also made use of properties with backing fields to make it possible to access a GameObject’s movement vector in different representations:

  • As a combination of length (speed) and angle
  • As a vector with x and y coordinates

In the context of a GameObject, that can look like the following, for example:

var speed by mutableStateOf(speed)
var angle by mutableStateOf(angle)
var position by mutableStateOf(position)
var movementVector
    get() = (Vector2.UNIT_X * speed).rotate(angle)
    set(value) {
        speed = value.length
        angle = value.angle()
    }

If we’re using this functionality outside of the GameObject class a lot, we could also consider defining additional length / angle getters and setters as extension properties on the Vector2 class, directly.

For our simulation, we still need to do a bit more – we haven’t yet addressed the problem of how to update location and speed based on the elapsed real time. Let’s talk about the approach for that next.

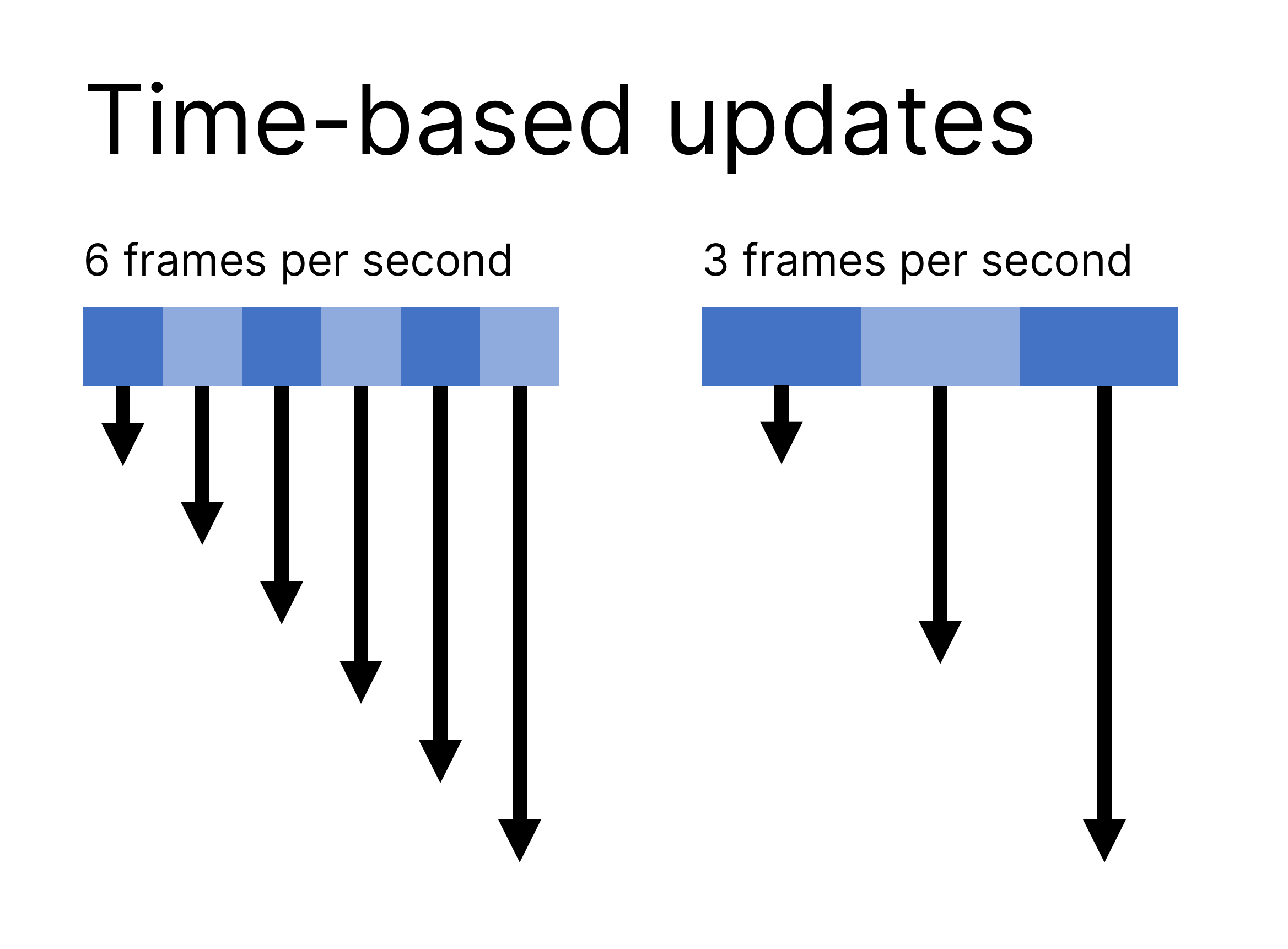
Frame-Independent Movement With Delta Timing

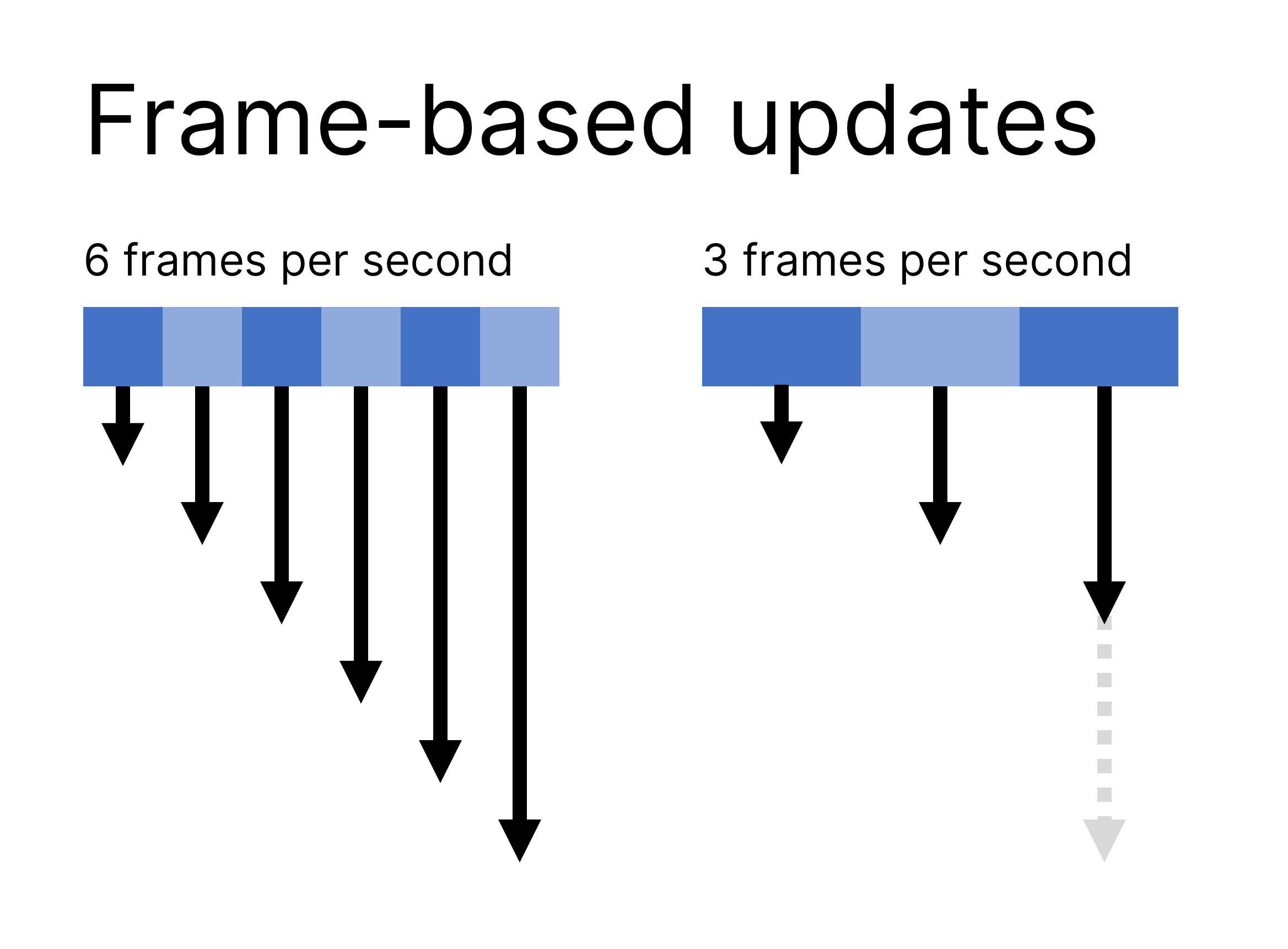
When building game logic, we need to keep one essential point in mind: Not all frames are created equal!

  • On a 60 Hz display, each frame is visible for 16ms.
  • On a 120 Hz display, that number drops to 8.3ms.
  • On a 240 Hz display, each frame only shows for 4.2ms.
  • On a system under load, or while running in a non-focused window, the application frame rate may be lower than 60 Hz.

That means that we can’t use “frames” as a measurement of time: If we define the speed of our spaceship in relation to the frame rate, it would move four times faster on a 240 Hz display than on a 60 Hz display.

frame-based

We need to decouple the game logic (and its rudimentary “physics simulation”) from the frame rate at which our application runs. Even AAA games don’t get this right all the time – but for our projects, we can do better!

A straightforward approach for this decoupling is to use delta timing: We calculate the new game state based on the time difference (the delta) since the last time we updated the game. This usually means we multiply the result of our calculations with the time delta, scaling the result based on the elapsed time.

time-based

In Compose for Desktop, we use withFrameMillis and withFrameNanos. Both of them provide a timestamp, so we just need to keep track of the previous timestamp to calculate the delta:

var prevTime = 0L

fun update(time: Long) {
    val delta = time - prevTime
    // . . .

In my case, a GameObject has an update function that takes a realDelta: Float:

val velocity = movementVector * realDelta.toDouble()
obj.position += velocity

As demonstrated in the code above, I use it to scale the velocity of game objects.

Closing Thoughts

This concludes our tour of building a small game with Compose for Desktop! To see how all the pieces fit together, read the source code (~300 lines of code) on GitHub!

Building Asteroids on Compose for Desktop was great fun! I am always surprised by the iteration speed that Compose for Desktop provides: Getting from a first rectangle to a full game in just one long evening.

Of course, implementing a retro game like Asteroids on modern hardware comes with the luxury of not having to think too hard about performance optimizations, allocations, entity-component systems, or more. When building something more ambitious, these points likely need addressing, and you might find yourself using a few additional libraries besides a Vector2 implementation.

For the next Super Hexagon, pixel roguelike, or other 2D game, however, you can definitely give Compose a shot.

Once again, you can find all 300 lines of source code for this project on GitHub.

If you’re looking for additional inspiration, take a look at some other folks building games with Compose!

Tags: